Tabung

Penjelasan lengkap apa itu benda yang berbentung tabung mulai dari rumus volume dan keliling, jaring-jaring, luas, ciri-ciri, dan sifatnya. Tabung atau silinder adalah bentuk tiga dimensi yang dibentuk oleh dua lingkaran paralel identik dan persegi panjang yang mengelilingi dua lingkaran. Silinder tersebut memiliki 3 sisi dan 2 rusuk. Kedua lingkaran ini disebut bagian bawah dan penutup atas, dan persegi panjang yang menutupinya disebut penutup tabung.

Tahun 1913, bidang dan entitas ditemukan oleh George Wentworth dan David Eugene Smith Geometri. Permukaan silinder adalah permukaan yang terdiri dari semua titik pada suatu garis, titik-titik ini sejajar dengan garis yang diketahui, dan melewati kurva bidang tetap dalam bidang yang tidak sejajar dengan garis yang ditentukan.

Pada garis ini, merupakan sekumpulan garis sejajar atau disebut juga elemen permukaan tabung. Dari sudut pandang kinematika, jika kurva bidang diberikan, itu disebut Directrix. Permukaan tabung adalah permukaan yang dilacak oleh garis yang disebut generatrix, bukan pada bidang Directrix yang sejajar dengan dirinya sendiri dan selalu melewati Directrix. Posisi spesifik dari matriks matriks adalah elemen permukaan tabung.

Bagian penampang pipa adalah permukaan pemotongan bidang dari pipa. Kurva adalah jenis penampang bidang. Bagian silinder yang berisi dua elemen dalam sebuah bidang disebut jajaran genjang dan bagian yang melingkar adalah selimut dasar persegi panjang.

Pipa tempat perpotongan bidang dan tegak lurus dengan semua elemen bagian pipa. Sisi kanan silinder berbentuk bulat, sehingga silinder tersebut berbentuk bulat. Umumnya, jika sisi kanan silinder adalah bagian kerucut (parabola, elips, hiperbola), silinder padat masing-masing disebut parabola, elips, dan hiperbola.

Silinder siku-siku dengan penampang elips. Eksentrisitas e dari penampang dan sumbu semi-mayor a dari penampang silinder bergantung pada jari-jari r dan sudut antara bidang yang berpotongan dan sumbunya :

Volume tabung

Bentuk botol minuman, botol termos dan kaleng makanan tidak jauh berbeda satu sama lain. Alas dan sungkup berbentuk bulat, sehingga badan induk berbentuk bujur sangkar yang menutupi alas dan sungkup.

Bentuk ini disebut tabung. Ruang arsitektural ini biasanya digunakan sebagai tempat menampung berbagai hal. Karena itu, jumlahnya cukup banyak. Untuk menghitungnya, kita membutuhkan rumus volume sebuah silinder.

Nah, pada kesempatan kali ini, kita akan mempelajarinya dan mengilustrasikan masalahnya dengan contoh. Mari kita mulai memahaminya.

Tabung dapat didefinisikan sebagai ruang sisi melengkung yang terdiri dari penutup dan alas yang berbentuk lingkaran dan ditutup pada sisi melengkung dari persegi panjang. Sekarang mari kita pelajari rumus volumenya.

Rumus Volume Tabung

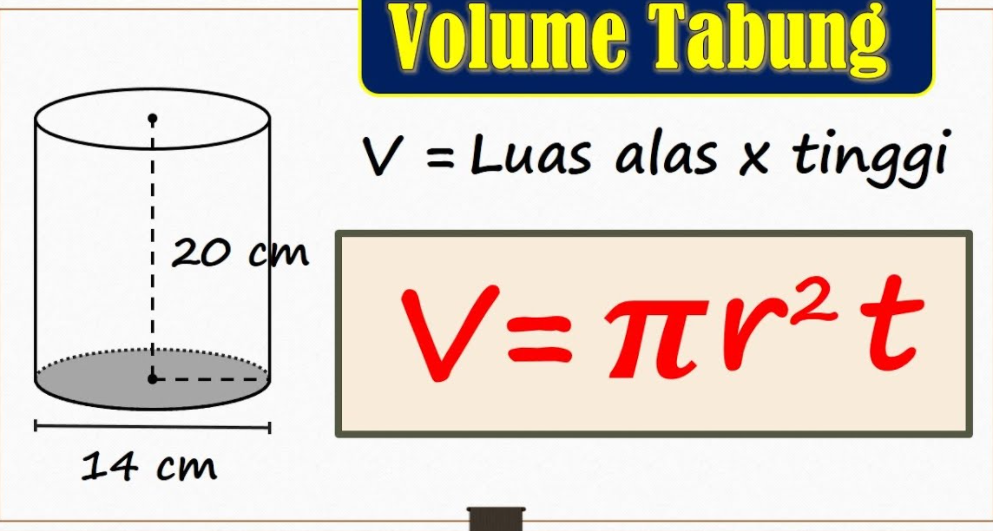
Sebelum kita mulai menghitung volume tabung, kita menghitung keliling dan luas permukaan :

Rumus keliling tabung

Jika kita punya kaleng dan ingin membukanya dengan pisau, pisau kita akan memotong tepi kaleng dan tepi kaleng. Ini disebut keliling alas atau keliling tutup. Lingkar dasar tabung adalah jarak yang dibutuhkan untuk mengelilingi dasar tabung. Bentuk lingkar pada dasar tabung sama rumusnya dengan rumus sama:

K = π x d

Keterangan:
K = keliling alas atau penutup
π = phi (22/7 atau 3,14)
d = diameter

Rumus luas permukaan tabung

Tabung tersusun dari tiga komponen yaitu dua buah lingkaran dan satu selimut. Bidang komposisi memiliki luas yang berbeda, dan luas bidang komposisi adalah

• Dasar atau penutup = πx r2
• Selimut = K x t

Luas permukaan tabung adalah dua kali luas lingkaran ditambah luas selimut, atau:

Luas permukaan = (2 x luas alas) + luas selimut

Keterangan:
K = keliling alas atau penutup
π = phi (22/7 atau 3,14)
r = jari-jari
t = tinggi tabung

Rumus volume tabung

Jika tabung reaksi terisi air, jumlah air yang dibutuhkan agar tabung reaksi terisi lengkap dinyatakan sebagai volume tabung reaksi. Volume sebuah tabung adalah kapasitas dari ruang yang ditampung tersebut. Rumus volumenya adalah:

V = luas alas x t

Informasi:
V = volume
t = tinggi

Contoh soal volume tabung

Sebuah silinder memiliki diameter 14 cm dan tinggi 10 cm. Berapa :

• Berapa panjang keliling?
• Luas permukaan?
• Kapasitas?

Jawaban:

Diameter nya adalah 14 cm, jadi jari-jarinya 7 cm

Keliling

K = πx d = 22/7 x 14 = 44 cm

Luas permukaan

Untuk mengetahui luas permukaan, Anda perlu menambah area dasar dan area cakupan pada lokasi berikut:

• Luas alas = πx r2 = 22/7 x 72 = 154 cm2
• Luas selimut = K x h = 44 x 10 = 440 cm2

Jadi luas permukaan = (2 x luas dasar) + luas cakupan = (2 x 154) + 440 = 308 + 440 = 748 cm2

Volume

Volume = luas alas x t = 154 x 10 = 1540 cm3

Jaring-jaring tabung

Cara membuat jaring-jaringnya:

1. Buat lingkaran atap dan alasnya berukuran sama, dan tentukan diameter atau radiusnya.
2. Tentukan panjang persegi panjang selimut kapas dengan metode berikut: Panjang = lingkar atas = 2 xπx r
3. Setelah itu, gabungkan semua sisi pipa sesuai dengan diagram jaringan di bawah, dan rekatkan atau pelapis lain untuk mengikatnya.

L = alas x tinggi (a x h)

Contoh Soal

Diketahui bahwa alas sebuah silinder berukuran 7 cm dan tingginya 12 cm. Temukan dan tutupi area jaringan pipa!

Yang diketahui:

alas = 7 cm
tinggi = 12 cm

Ditanya: area = …?

Jawaban:

L = a x t
P = 7cm x 12cm
L = 84 sentimeter persegi
Oleh karena itu, luasnya = 84 sentimeter persegi

Diketahui ada pipa dengan bagian bawah 5 cm dan tinggi 20 cm. Temukan dan tutupi area jaringan pipa!

Yang diketahui:

alas = 5 cm
tinggi = 20 cm
ditanya: area = …?

Jawaban:

L = a x t
P = 5cm x 20cm
L = 100 sentimeter persegi
Oleh karena itu, luasnya = 100 sentimeter persegi

Benda berbentuk tabung

Membahas tentang ilmu bangun ruang untuk siswa kelas 1-3 SD. Ini adalah sebuah pertanyaan : benda berbentuk tabung di dalam rumah yaitu: toples, celengan koin, gelas, botol air.

Karakteristik

1. Memiliki 3 sisi yaitu alas, penutup dan selimut (sisi vertikal).
2. Terdapat alas dan tutup melingkar.
3. Ada sisi tegak berupa bidang melengkung yang disebut dengan selimut tabung.
4. Terdapat 2 rusuk: bawah dan atas (penutup).
5. Memiliki tinggi: jarak antara pusat alas dan pusat tutupnya.
6. Bagian bawah tabung dan tutupnya memiliki radius yang sama.

Sifat-sifat

Salah satu bentuk ruang yang juga harus diketahui siswa adalah silinder. Bentuk tabung atau biasa disebut silinder sebenarnya bukanlah bentuk yang “aneh”. Dalam kehidupan kita, banyak benda disekitarnya berbentuk silinder. Beberapa contoh termasuk drum, kendi susu, toples, dll. Oleh karena itu, bentuk datar ini sebaiknya dimasukkan ke dalam benda konkret saat mempelajari dan memperkenalkannya agar siswa dapat mengacu pada ciri-cirinya.

Ciri-ciri yang harus diketahui adalah:

1. Bagian bawah dan atas berbentuk bulat dan berukuran sama.
2. Dengan 3 sisi yaitu alas, atap dan selimut.
3. Tidak ada puncak.
4. Memiliki 2 rusuk, yaitu rusuk yang mengelilingi bagian bawah dan atas.

Ketinggian silinder adalah garis vertikal yang menghubungkan tengah bawah dan tengah atas. Tinggi silinder diwakili oleh t, dan jari-jari alas diwakili oleh r. Seperti bentuk lainnya, untuk menghitung volume tabung, gunakan rumus berikut:

Volume = luas alas x tinggi

Karena bagian bawah berbentuk bulat, luasnya dihitung menggunakan rumus lingkaran πr2

Oleh karena itu, volume silinder = πr2t

Luas pipa blanket dapat dihitung dengan menjumlahkan luas permukaan alas dan atap dengan luas permukaan pipa blanket.

Selimut tabung akan membentuk persegi panjang jika diregangkan yang panjangnya ditentukan oleh keliling lingkaran alas / atap, dan tingginya adalah tinggi tabung. Oleh karena itu, luas penutup adalah 2πrt.

Jadi luas permukaan = 2πr2 + 2πrt = 2πr (r + t)